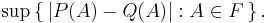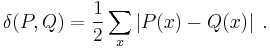Total variation distance of probability measures

In probability theory, the total variation distance between two probability measures P and Q on a sigma-algebra F is

$\sup\left\{\,\left|P(A)-Q(A)\right|�: A\in F\,\right\}.$

Informally, this is the largest possible difference between the probabilities that the two probability distributions can assign to the same event.

For a finite alphabet we can write

$\delta(P,Q) = \frac 1 2 \sum_x \left| P(x) - Q(x) \right|\;.$

Sometimes the statistical distance between two probability distributions is also defined without the division by two.

The total variation distance is related to the Kullback–Leibler divergence by Pinsker's inequality.

References